提要

数据资产时代拉开帷幕，数据资产入表已成为激活新质生产力的核心驱动力。开鑫科技积极响应时代需求，已落地多项数据资产入表项目，涵盖交通出行、公共管理、医疗健康、文化旅游等行业领域。

 

在业务实践中，开鑫科技深刻认识到数据价值评估对资产入表的关键作用。传统评估方法如成本法、收益法或市场法，往往难以全面反映数据内在价值。基于理论探索与实战经验，我们初步形成一套融合机器学习和夏普利值的创新方案，为数据价值评估提供了可量化、可解释的新路径。

 

 

01背景

机器学习（Machine Learning）是人工智能的子领域，它利用统计方法让模型自发从数据中发现规律，进而对未知数据进行判断或预测。数据价值通常都需要在具体场景中发掘，而很多场景可以用机器学习来实现。例如，对地段数据运用回归模型来预测房价，或是对植物特征数据运用分类模型来判断种类。

 

夏普利值（Shapley Value）是合作博弈的经典概念，它在考虑联盟参与者相互间开展合作博弈的所有情形后，以简洁的数学公式对每个参与者的贡献给予数学上公平的评价。夏普利值的公式有多种，其中之一如下所示：

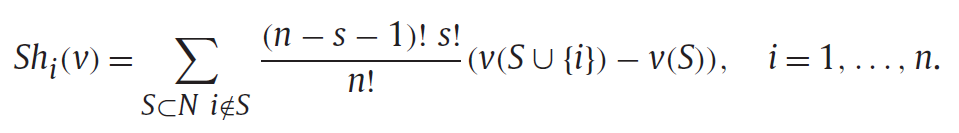
夏普利值计算较为复杂，但其含义清晰、解释性强。如果我们能构建从真实场景到机器学习模型的映射框架，将数据转化为合作博弈下的“联盟参与者”，那么就能运用夏普利值来计算各项数据对模型效果的贡献，进而评估数据的质量或价值。

 

02应用

如果有两个数据集，各有近万条数据，应用场景是通过某种机器学习模型进行回归，以预测某种数值，如何判断哪一个的价值更大？

 

一种比较简单的方法是看哪个数据集大，即哪个数据集数据更多，哪个价值就更大。这样做的前提是两个数据集质量差不多，如果数据集质量差异比较大，那么大小就很可能不是决定因素。

 

另一种常见的方法是投入到模型中看预测效果。比如，数据集1在回归模型训练后预测的R方评分是0.79，数据集2则是0.85，根据这个结果，数据集2比数据集1更好，那么评分高低能反映两者的价值差异吗？

 

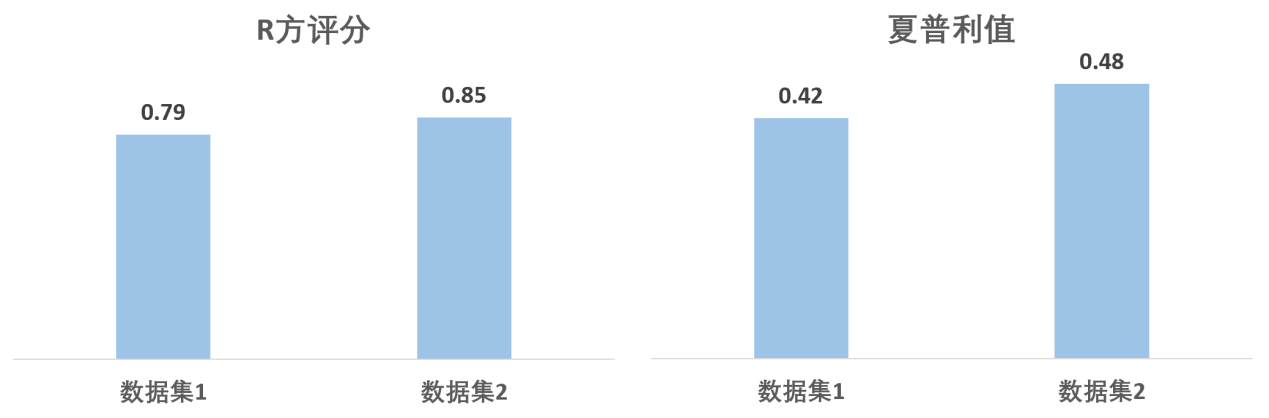
图1：数据的功能与价值

 

夏普利值综合考虑了两者在所有可能情形的贡献，能提供定量的比较结果。通过计算，我们得出数据集1的夏普利值是0.42，数据集2是0.48。两者夏普利值的差异为14.3%，明显高于R方评分的差异7.7%，这是由于R方评分是单一角度的计算，并未考虑所有可能情形。若针对这两个数据集开展采购决策，夏普利值可为资金分配提供量化依据。基于夏普利值，数据集2应当更贵，而且要比数据集1贵14.3%。

 

我们甚至可以计算数据点（单条记录）的夏普利值，以更精细的反映数据价值。对于简单的机器学习模型及较小的数据集，可逐点计算数据价值。有些场景模型简单，但数据稀有而很难获得，就可以这样处理。比如，有一个简单的分类模型（SVM），数据样本比较有限，新获取30个数据点，那么就可以逐个评估这些新增数据点的价值。

 

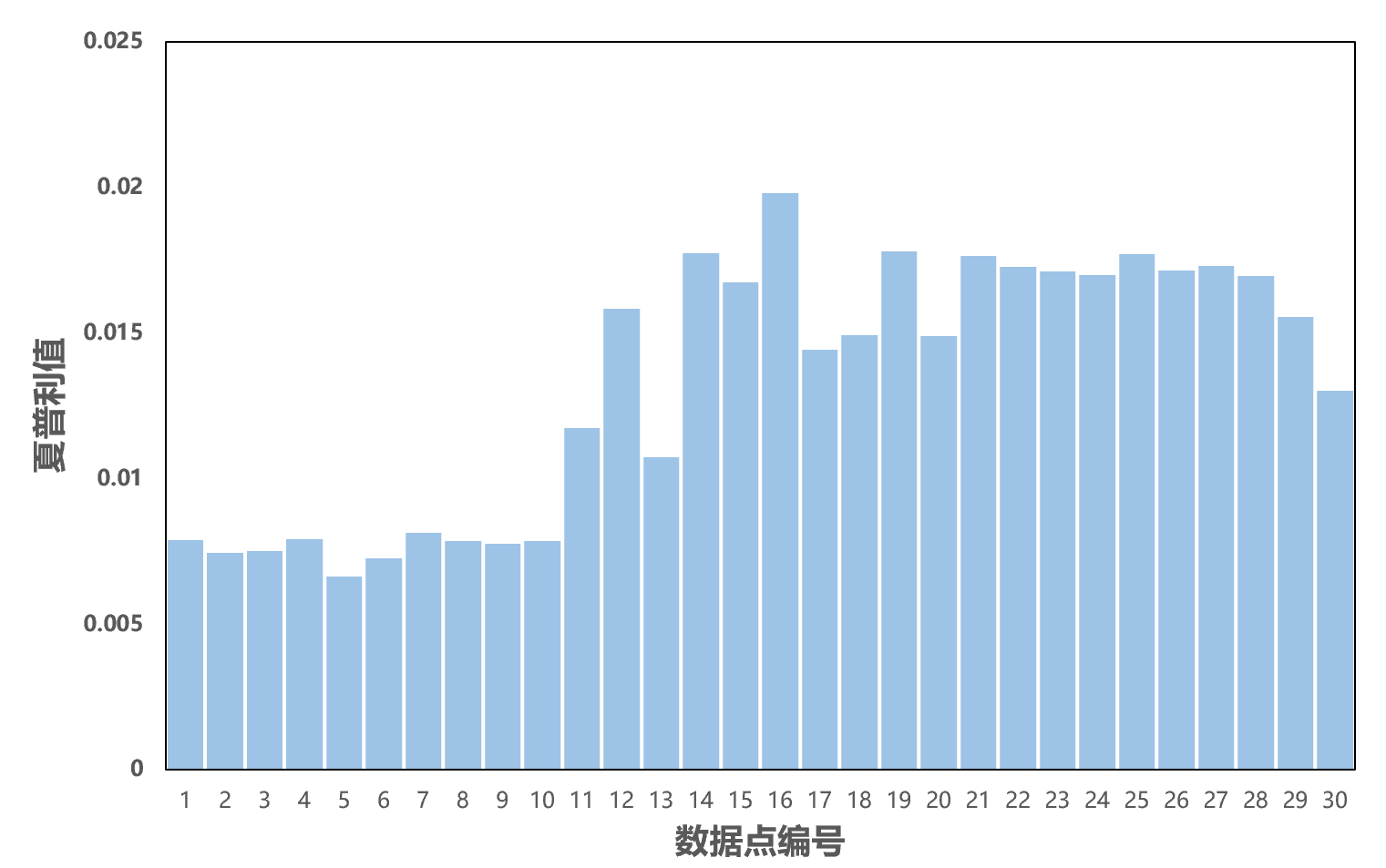
图2：逐点计算的夏普利值

 

夏普利值显示，数据点对于训练的贡献存在差异，有的很突出，有的比较有限。其中，价值最高的点是第16个，最低的是第5个，前十个数据点整体上不如后二十个数据点价值高，平均价值相差一倍。

 

很多时候，数据集非常庞大，所用的模型也比较复杂，导致夏普利值的计算速度极为缓慢。这时逐点计算既不现实也无必要，就可以换一种思路，计算数据集内部不同数据子集的夏普利值。由此我们既可以比较同类数据集相互之间的价值差异，也可以对数据集内部进行结构性的价值分析。比如，将一个大的数据集按顺序拆成10个子集，结合特定模型计算这些子集的夏普利值，可以了解它们在整个数据集中的贡献，以及数据集内部的价值分布，如下图所示：

 

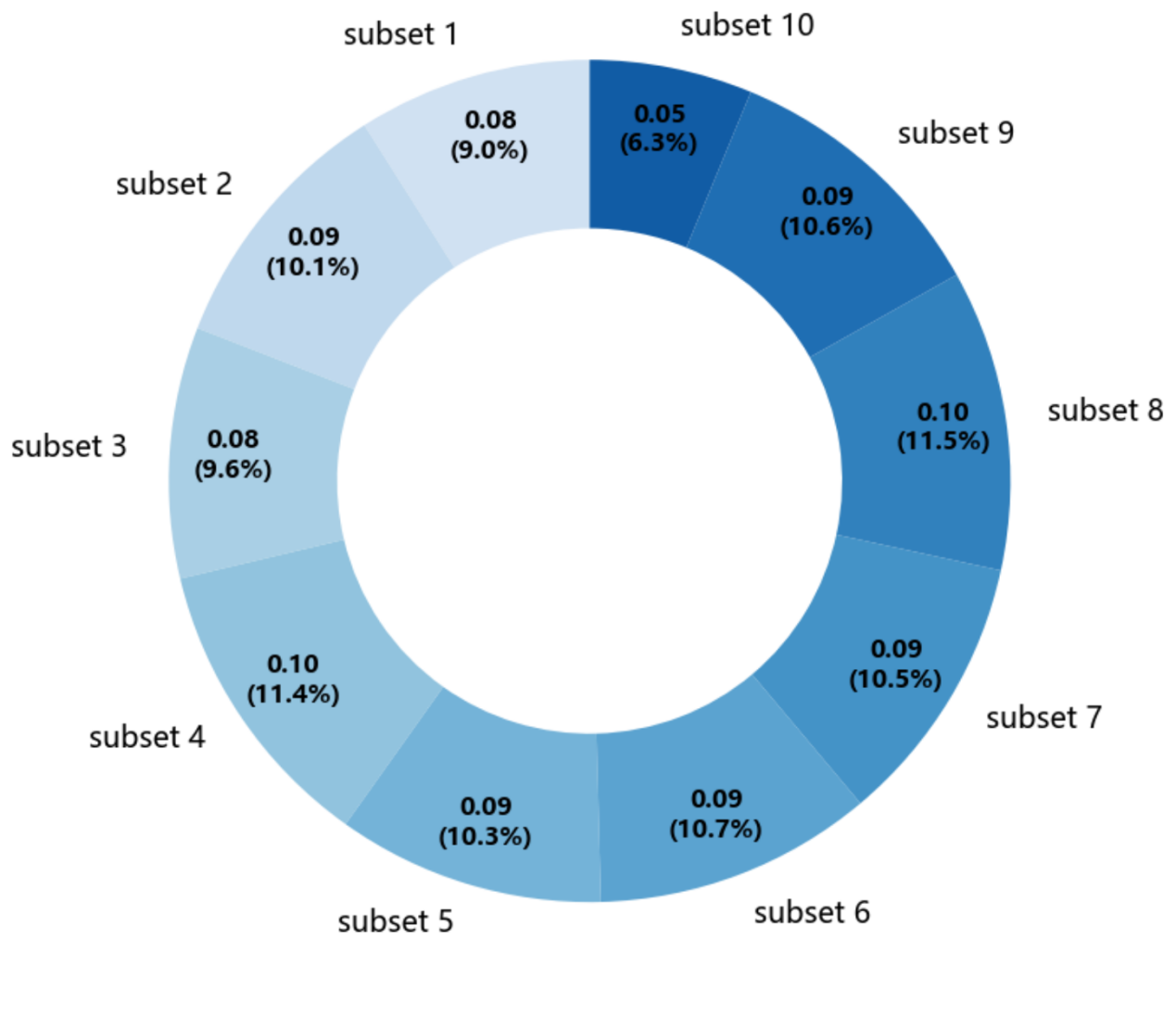
图3：数据集内部的价值分布

 

 

03优势

 

机器学习与夏普利值的融合，拓展了数据价值评估的技术边界，为传统成本法、收益法等评估方式提供了创新性补充与参照。随着场景化数据交易规模的持续扩大、算法精度的迭代优化及计算机性能的跃升，这一评估方法的应用场景将不断拓展，进而嵌入数据资产入表、运营、融资或资本化等环节，深度赋能新质生产力。

 

相较于传统评估方法，该方案通过技术融合形成了四大显著优势：

 

01场景针对性强

通过机器学习与具体场景或用途构建联系

02为数据价值比较提供量化手段

运用夏普利值来公平表达数据集或数据点的贡献

03探索数据内含价值

从数据子集或数据点层面来展示数据价值的结构性分布

04为数据选择、使用和购买提供参考依据

从博弈论视角深化对数据价值的认知，为决策提供理论支撑

 

参考文献

1. Shapley, L. S. (1953) A value for n-person games.

2. Fatima, S. S., Wooldridge, M., Jennings, N. R. (2008) A linear approximation method for the Shapley value.

3. Castro, J., G´omez, D., Tejada, J. (2009) Polynomial calculation of the Shapley value based on sampling.

4. Lundberg, S. M., Lee, S. (2017) A unified approach to interpreting model predictions.

5. Chen, L., Koutris, P., Kumar, A. (2019) Towards Model-based Pricing for Machine Learning in a Data Marketplace.

6. Ghorbani, A., Zou, J. Y. (2019) Data Shapley: Equitable Valuation of Data for Machine Learning.

7. Veldkamp, L. (2023) Valuing Data as an Asset.